Absolute Value
Absolute Values represented using two |'s are common in Algebra. They are meant to signify the number's distance from 0 on a number line. So, if the number is negative, it becomes positive. And if the number was positive, it remains positive:
|8| = 8 and |−8| = 8
A formal definition of |x| is:
If x ≥ 0, then |x| = x
If x ≤ 0, then |x| = −x
If x ≤ 0, then |x| = −x
Graphical Representation of |x| using formal definition provided above:
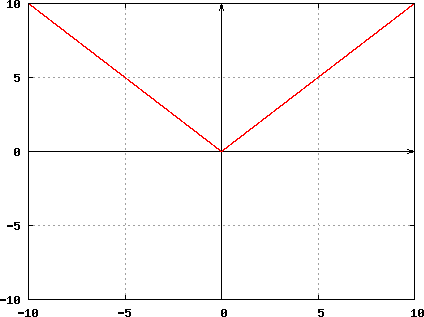
Properties:

Example #1:
Find x for |x| =19
As the absolute value of either +19 or −19 will result in 19, it follows that x = −19 or 19
Solution #1:
As the absolute value of either +19 or −19 will result in 19, it follows that x = −19 or 19
Example #2:
Find x for
|3x + 9| = 6
Knowing that the contents within the absolute value symbol should equal 4, it follows that:
3x + 9 = 6 and 3x +9 = −6
∴ x = −1, −5
Solution #2:
Knowing that the contents within the absolute value symbol should equal 4, it follows that:
3x + 9 = 6 and 3x +9 = −6
∴ x = −1, −5
Example #3:
Find x for −2 |3x + 9| = 6
Dividing both sides by -2, results in the following:
|3x + 9| = −2
As an absolute value can never be negative, correct answer is 'No Solution'
Solution #3:
Dividing both sides by -2, results in the following:
|3x + 9| = −2
As an absolute value can never be negative, correct answer is 'No Solution'


