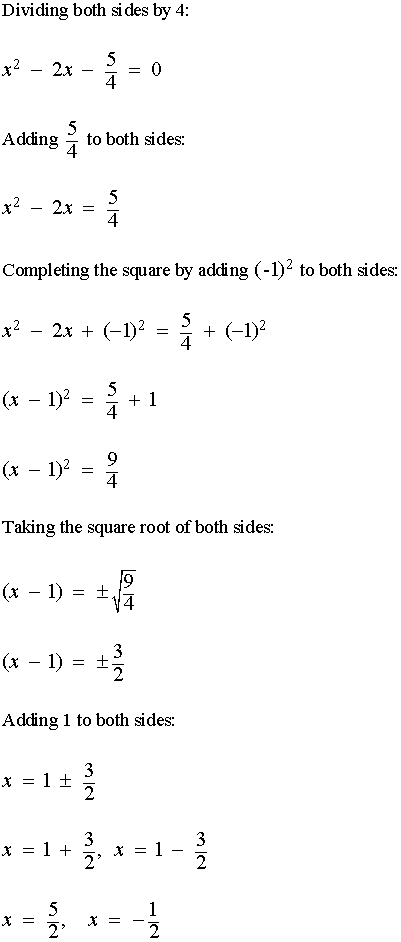Completing the Square
A method for solving quadratic equations concerns a technique called "completing the square" which is based upon the concept of creating an equation containing a perfect square. A perfect square represents a polynomial, which is the square of another polynomial. As an example, x2 + 8x + 16 is a perfect square of x + 4 since x2 + 8x + 16 equals (x + 4)2. Consequently, if one side of an equation contained x2 +8x, a perfect square could be attained by adding 16 to both sides of the equation to attain (x + 4)2.
More generally, completing the square may be accomplished by adding (c/2)2 to x2 + cx, where c = constant.

Example:
Solve the equation 4x2 − 8x − 5 = 0
Solution: