Matrices
A matrix is a rectangular table of elements (or entries), which may be numbers or, more generally, any abstract quantities that can be added and multiplied.
The horizontal lines in a matrix are called rows and the vertical lines are called columns. A matrix with m rows and n columns is called an m-by-n matrix (written m × n) and m and n are called its dimensions.
The dimensions of a matrix are always given with the number of rows first, then the number of columns. It is commonly said that an m-by-n matrix has an order of m × n ("order" meaning size). Two matrices of the same order whose corresponding entries are equivalent are considered equal.

Almost always capital letters denote matrices with the corresponding lower-case letters with two indices representing the entries. For example, the entry of a matrix A that lies in the i-th row and the j-th column is written as ai,j and called the i,j entry or (i,j)-th entry of A. Alternative notations for that entry are A[i,j] or Ai,j. The row is always noted first, then the column.
A matrix where one of the dimensions equals one is often called a vector, and interpreted as an element of real coordinate space. An m × 1 matrix (one column and m rows) is called a column vector and a 1 × n matrix (one row and n columns) is called a row vector.
Matrix Addition:
Two or more matrices of identical dimensions m and n can be added. Given m-by-n matrices A and B, their sum A+B is the m × n matrix computed by adding corresponding elements.
Example:
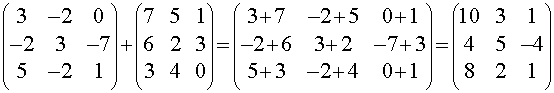
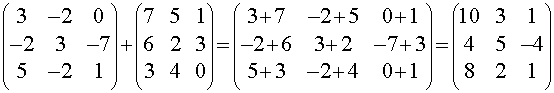
Matrix Subtration:
Similar to matrix addition as described above, two or more matrices of identical dimensions m and n can be subtracted. Given m × n matrices A and B, their sum A-B is the m × n matrix computed by adding corresponding elements.
Scalar Mulitplication:
Given a matrix A
and a number c, the scalar multiplication cA
is computed by multiplying every element of A by
the scalar c.
Example:
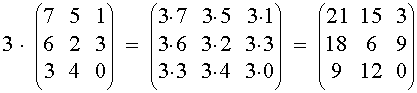
Matrix Multiplication:
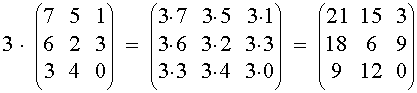
Matrix Multiplication:
Multiplication
of two matrices is well-defined only if the number of columns of the
left matrix is the same as the number of rows of the right matrix. If A
is an m × n
matrix and B is an m × n
matrix, then their matrix
product AB is the m ×
p matrix given by:
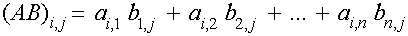
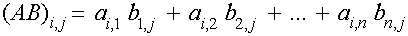
Matrix multiplication has the following properties:
- (AB)C = A(BC) for all k × m matrices A, m × n matrices B and n × p matrices C
- (A+B)C = AC+BC for all m × n matrices A and B and n × k matrices C
- C(A+B) = CA+CB for all m × n matrices A and B and k × m matrices C
Matrix multiplication is not commutative; that is, given matrices A and B and their product defined, then generally AB ≠ BA. It may also happen that AB is defined but BA is not defined.
Related Topics:


