Using Laplace Transforms to Solve Linear Differential Equations
Laplace transforms may be used to solve linear differential equations with constant coefficients by noting the nth derivative of f(x) is expressed as:
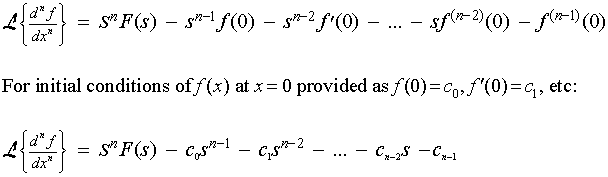
Conseqently, Laplace transforms may be used to solve linear differential equations with constant coefficients as follows:
- Take Laplace transforms of both sides of equation using property above to express derivatives
- Solve for F(s), Y(s), etc.
- Take inverse Laplace transform to attain ultimate solution of equation
Example:
Solve y' − 3y = e3x, y(0) = 0
Solution:
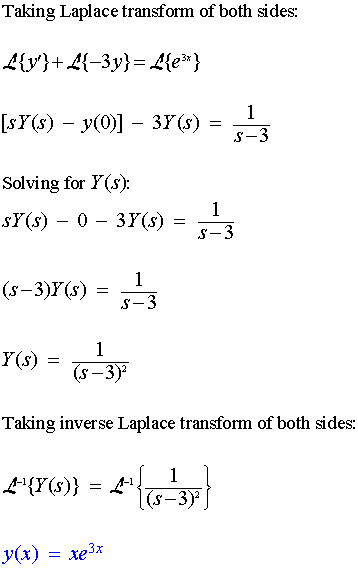
Related Topics:
Related Topics:


