Wronskian
Given a set of n functions f1, ..., fn, the Wronskian W(f1, ..., fn) is given by:
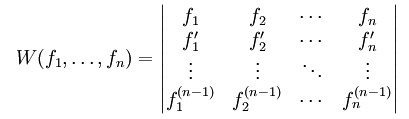
The Wronskian can be used to determine whether a set of differentiable functions is linearly independent on a given interval:
- If the Wronskian is non-zero at some point in an interval, then the associated functions are linearly independent on the interval.
The Wronskian is particularly beneficial for determining linear independence of solutions to differential equations. For example, if we wish to verify two solutions of a second-order differential equation are independent, we may use the Wronskian, which requires computation of a 2 x 2 determinant.
Note: If the Wronskian is uniformly zero over the interval, the functions may or may not be linearly independent. A common misconception is that W = 0 everywhere implies linear dependence.
Example:
Find the Wronskian for the functions sin x and cos x. Using value of the Wronskian, determine whether the functions are linearly independent.
Solution:




