Circles: Products of Secants
For secants intersecting a circle, the product of entire secant length times the length corresponding to its interior porition will be the same for each secant.
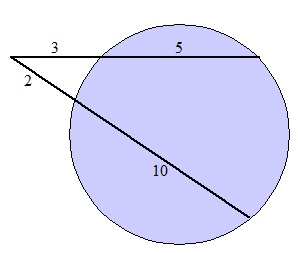
In the figure above, the product for segment of each chord equal 24:
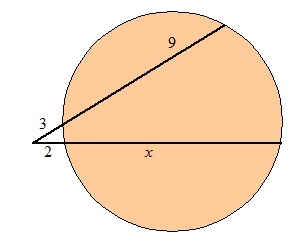
Find the length of the chord, x, in the illustration below:
Solution:
x = 16
- First Secant: (3 + 5)(3) = (8)(3) = 24
- Second Secant: (2 + 10)(2) = (12)(2) = 24
Example:
Find the length of the chord, x, in the illustration below:

Solution:
The chord, x, corresponds to the inner portion of the bottom secant.
Using products of secants, it follows that:
(3)(3 + 9) = 2(2 + x)
(3)(12) = 4 + 2x
36 = 4 + 2x
32 = 2x
Using products of secants, it follows that:
(3)(3 + 9) = 2(2 + x)
(3)(12) = 4 + 2x
36 = 4 + 2x
32 = 2x
x = 16
Related Topics:


