Chi-Square Distribution
The Chi-Square distribution is a special case of the Gamma distribution. The Chi-Square distribution serves a significant role in the Chi-Square test, which is used to determine goodness of fit between an observed distribution and a theoretical one.
The probability density function of the Chi-Square distribution is defined by:
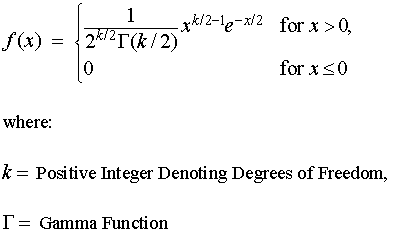
The probability density function of the Chi-Square distribution for k degrees of freedom ranging from one through five is plotted below:
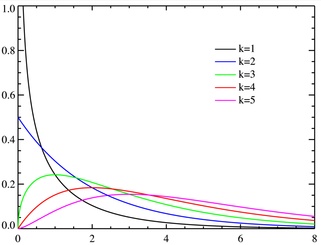
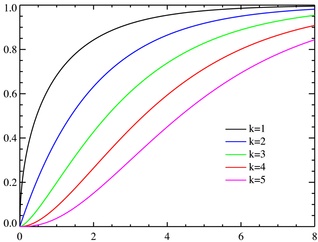
Additionally, the cumulative distribution function f the Chi-Square distribution for
k degrees of freedom ranging from one through five is provided below:
Various attributes of the Chi-Square distribution are listed below:
- Mean = k
- Median ≈ k − 2/3
- Mode = k − 2 for k ≥ 2
- Variance = 2k
Related Topics:
- Chi-Square Test
- Gamma Function


