Geometric Distribution
The geometric distribution is the negative binomial distribution with k = 1:
Pr(X = n) =
p(1 − p)n−1
where:
n = Number of trials necessary to obtain a success
p = Probability of success for each independent trial
The mean and variance for the negative binomial distribution are:
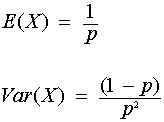
Example:
For geometric random variable X
with p =
0.4, what is Pr(X ≤ 3)?Solution:
Pr(X ≤ 3) =
Pr(X = 1) + Pr(X = 2) + Pr(X = 3)
Pr(X ≤ 3) = p(1 − p)1−1 + p(1 − p)2−1 + p(1 − p)3−1
Pr(X ≤ 3) = p(1 − p)1−1 + p(1 − p)2−1 + p(1 − p)3−1
Pr(X ≤ 3) = p(1 − p)0 + p(1 − p)1 + p(1 − p)2
Pr(X ≤ 3) = p + p(1 − p) + p(1 − p)2
Since p = 0.4:
Pr(X ≤ 3) = 0.4 + (0.4)(1 − 0.4) + (0.4)(1 − 0.4)2
Pr(X ≤ 3) = 0.4 + (0.4)(0.6) + (0.4)(0.6)2
Pr(X ≤ 3) = 0.4 + 0.24 + 0.144
Pr(X ≤ 3) = 0.784
Related Topics:


