Markov's Inequality
Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant.
For a > 0:
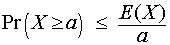
Markov's inequality is used
to present another significant proportion entitled Chebyshev's
inequality.
Example:
For random variable X greater than with
a binomial
distribution with probability of success equal to 0.3 and
number of trials equal to 100, determine the upper bound regarding
probability of X
greater than or equal to 50 using Markov's inequality.
Solution:
Given the following
values for Binomial distribution:
p = Probability of success = 0.3
N = Number of trials = 100
For Binomial distribution:
E(X) = Np = (100)(0.3) = 30
Using Markov's inequality:
Pr(X ≥ 50) ≤ 30/50 or
Pr(X ≥ 50) ≤ 0.6
p = Probability of success = 0.3
N = Number of trials = 100
For Binomial distribution:
E(X) = Np = (100)(0.3) = 30
Using Markov's inequality:
Pr(X ≥ 50) ≤ 30/50 or
Pr(X ≥ 50) ≤ 0.6


