Skip to content
Resources

    Chebyshev's Inequality


    Chebyshev's inequality may be used to determine the likelihood regarding closeness of the value of a particular random variable relative to its mean.

    For random variable X with mean μ and variance σ2:



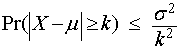
    Example #1:

    For random variable X greater than with a binomial distribution with probability of success equal to 0.3 and number of trials equal to 100, determine the upper bound regarding probability of X residing between 20 and 40 using Chebyshev's inequality.

    Solution #1:
    Given the following values for Binomial distribution:

    p = Probability of success  = 0.3

    N = Number of trials = 100

    For Binomial distribution:

    E(X) = Np = (100)(0.3) = 30

    Var(X) = σ2 = Np(1 − p) = (100)(0.3)(0.7) = 21

    Using Chebychev's inequality:

    Pr(|X − 30| ≥ k) ≤ 21/k2

    Pr[(X ≥ 30 + k) or (X ≤ 30 − k)]  ≤ 21/k2

    Using k = 10:

    Pr[(X ≥ 30 + 10) or (X ≤ 30 − 10)]  ≤ 21/102

    Pr[(X ≥ 40) or (X ≤ 20)]  ≤ 0.21

    Knowing Pr[(X ≥ 40) or (X ≤ 20)] + Pr[(20 <  X  < 40)] = 1:

    Pr[(20 <  X  < 40)] = 1 − Pr[(X ≥ 40) or (X ≤ 20)]

    Pr[(20 <  X  < 40)] = 1 − 0.21

    Pr[(20 <  X  < 40)] = 0.79


    Example #2:

    Determine the maximum probability that values of a random variable would deviate two or more standard deviations from its mean.
    Solution #2:
    Using Chebyshev's inequality with k = 2σ:

    Pr(|X − μ| ≥ 2σ) ≤ σ2/(2σ)2

    Pr(|X − μ| ≥ 2σ) ≤ σ2/4σ2

    Pr(|X − μ| ≥ 2σ) ≤ 1/4 or

    Pr(|X − μ| ≥ 2σ) ≤ 0.25
    Related Topics: