Polar Coordinate System
The polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by an angle and a distance. The polar coordinate system is especially useful in situations where the relationship between two points is most easily expressed in terms of angles and distance.
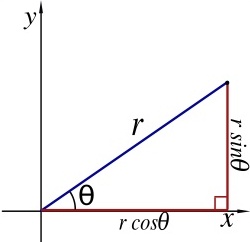
As the coordinate system is two-dimensional, each point is determined by two polar coordinates: the radial coordinate and the angular coordinate. The radial coordinate (usually denoted by r) denotes the point's distance from a central point known as the pole (equivalent to the origin in the Cartesian system). The angular coordinate (also known as the polar angle and usually denoted by θ or t) denotes the positive or counterclockwise angle required to reach the point from the 0° ray or polar axis (equivalent to the positive x-axis in the Cartesian coordinate plane).
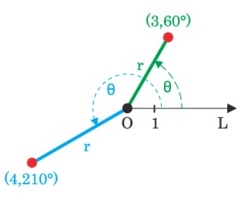
As an example, the polar coordinates (3, 60°) and (4, 210°) are plotted as points in the figure below:
Converting Between Polar and Cartesian Coordinate Systems
The polar coordinates r and θ can be
converted to the Cartesian coordinates x and y by using
the trigonometric functions sine and cosine:
Furthermore, the x and y Cartesian coordinates may be converted to the polar coordinate r using the following:
x = r sin θ
y = r cos θ
y = r cos θ
To determine the angular coordinate θ, the following two ideas must be considered:
- For r = 0, θ can be set to any real value
- For r ≠ 0, to get a unique representation for θ, it must be limited to an interval of size 2π. Conventional choices for such an interval are [0, 2π) and (−π, π]
Furthermore, the x and y Cartesian coordinates may be converted to the polar coordinate r using the following:
r2 = x2 + y2