Conic Sections: Hyperbola
A hyperbola is defined as the locus of points where the difference in the distance to two fixed points (called foci) is constant. That fixed difference in distance is two times a where a is the distance from the center of the hyperbola to the vertex of the nearest branch of the hyperbola. a is also known as the semi-major axis of the hyperbola. The foci lie on the transverse axis and their midpoint is called the center.
In an x-y coordinate system, the hyperbola opening east-west with center (h,k) along with semi-major axis, a, and semi-minor axis b is represented by:
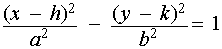
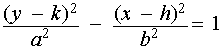
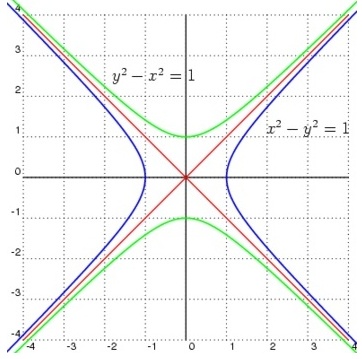
In the above figure, the blue colored hyperbola opens east-west while the light green colored hyperbola opens north-south.
Eccentricity of Hyperbola:
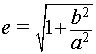
The foci for an east-west opening hyperbola are given by
(h ± c, k) where c2 = a2 + b2
and for a north-south opening hyperbola are given by
(h, k ± c) where c2 = a2 + b2
Hyperbolas In Polar Coordinates:
East-west opening hyperbola:
r2 = a sec 2θ
North-south opening hyperbola:
r2 = −a sec 2θ
Northeast-southwest opening hyperbola:
r2 = a csc 2θ
Northwest-southeast opening hyperbola:
r2 = −a csc 2θ
In all formulas the center is at the pole, and a is the semi-major axis and semi-minor axis.
Hyperbolas In Parametric Form:
East-west opening hyperbola:
x = a sec t + h, y = b tan t + k
or
x = ± a cosh t + h, y = b sinh t + k
North-south opening hyperbola:
x = a tan t + h, y = b sec t + k
or
x = a sinh t + h, y = ±b cosh t + k
In all formulae (h,k) is the center of the hyperbola, a is the semi-major axis, and b is the semi-minor axis.


