Skip to content
Resources

    Functions: Even and Odd Functions


    Even functions and odd functions are functions which satisfy particular symmetry relations, with respect to additive inverses.
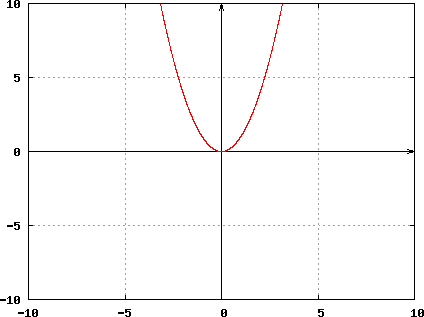
    Even Functions:

    Let f (x) be a real-valued function of a real variable. Then f is even if the following equation holds for all x in the domain of f:

    f (x) = f (−x)

    Geometrically, an even function is symmetric with respect to the y-axis, meaning that its graph remains unchanged after reflection about the y-axis.  An example of an even function, f(x) = x2, is illustrated below:


    Odd Functions:

    Let f(x) be a real-valued function of a real variable. Then f is odd if the following equation holds for all x in the domain of f:

    − f (x) = f (−x)

    Geometrically, an odd function is symmetric with respect to the origin, meaning that its graph remains unchanged after rotation of 180 degrees about the origin.  An example of an even function, f (x) = x3, is illustrated below:



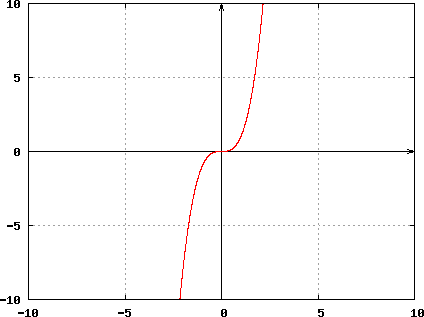
    Properties Relating to Odd and Even Functions
    • The only function which is both even and odd is the constant function which is identically zero (i.e., f (x) = 0 for all x).
    • The sum of an even and odd function is neither even nor odd, unless one of the functions is identically zero.
    • The sum of two even functions is even, and any constant multiple of an even function is even.
    • The sum of two odd functions is odd, and any constant multiple of an odd function is odd.
    • The product of two even functions is an even function.
    • The product of two odd functions is again an even function.
    • The product of an even function and an odd function is an odd function.
    • The quotient of two even functions is an even function.
    • The quotient of two odd functions is an even function.
    • The quotient of an even function and an odd function is an odd function.
    • The derivative of an even function is odd.
    • The derivative of an odd function is even.
    • The composition of two even functions is even, and the composition of two odd functions is odd.
    • The composition of an even function and an odd function is even.
    • The composition of any function with an even function is even (but not vice versa).

    An example of a function which is neither even nor odd is

         f (x) = x3 +5 as:

         f (−x)  =  (−x)3 +5  =  (−1)3x3 + 5  =  −x3 + 5

    −f(x)  =  −(x3 + 5)  =  −x3 − 5

    Clearly,     f (−x) ≠ −f (x) for all x in the domain of f (x)
    Related Topics: