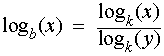Logarithms
A logarithm (to base b) of a number x is the exponent y that satisfies x = by. It is written logb(x) or, if the base is implicit, as log(x). Mathematically, expressed as:
y =
logb(x) or x = by
Examples:
35 = 3 x 3 x 3 x 3 x 3 = 243 and log3(243) = 5
103 = 10 x 10 x 10 = 1000 and log10(1000) = 3
Examples:
35 = 3 x 3 x 3 x 3 x 3 = 243 and log3(243) = 5
103 = 10 x 10 x 10 = 1000 and log10(1000) = 3
Common Bases:
Change of Base:
- Natural logarithm (loge(x), ln(x), log(x), or Ln(x)) where e » 2.71828...
- Common logarithm (log10(x) or simply log(x); occasionally lg(x))
- Binary logarithm (log2(x); occasionally lg(x), lb(x) or ld(x))
Logarithmic Identities:
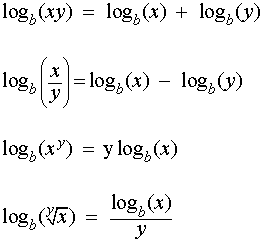
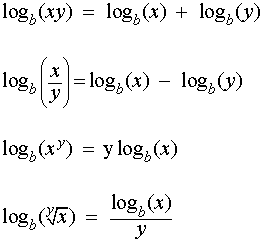
Change of Base: