Real Functions: Root Functions
An root function is a function expressed by x1/n for positive integer n greater than 1. The graphical representation of power functions is dependent upon whether n is even or odd.
For even values of n (i.e., n = 2, 4, 6, ...), root functions will resemble the form illustrated for square root function expressed by f (x) = x1/2 depicted below:
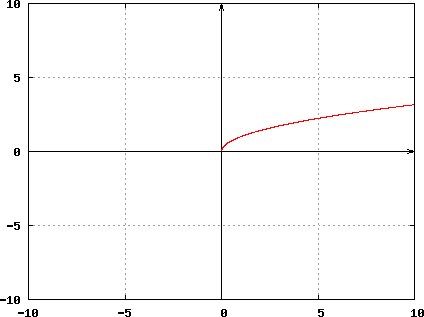
Clearly, root functions
with even numbers for n, only permit values of x ≥ 0.
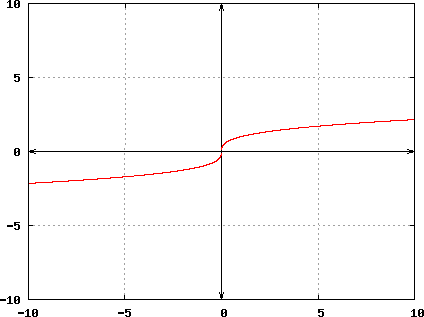
Similarly, for odd values of n greater than 1 (i.e., n = 3, 5, 7, ...), root functions will resemble the form illustrated for cube root function expressed by f (x) = x1/3 depicted below:
Similarly, for odd values of n greater than 1 (i.e., n = 3, 5, 7, ...), root functions will resemble the form illustrated for cube root function expressed by f (x) = x1/3 depicted below: