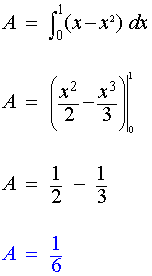Integrals: Area Between Curves
For f (x) and g(x) integratable over interval I = [a,b], the area between curves is defined as:
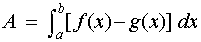
Example:
Find the area of the region bounded by the curves y = x and y = x2
Solution:
In order to determine the region bounded by the
two curves, it is necessary to find their points of intersection.
Using y = x and y = x2, it follows that:
x2 = x
x2 − x = 0 (Attained by subtracting x from both sides)
Using y = x and y = x2, it follows that:
x2 = x
x2 − x = 0 (Attained by subtracting x from both sides)
x(x −
1) = 0
x = 0 or x = 1
Using y = x and y = x2, it follows that y = 0 when x = 0 and y = 1 when x = 1
∴ Points of intersection between the two curves are (0,0) and (1,1)
Using intersection points, the region bounded by the two curves becomes;
x = 0 or x = 1
Using y = x and y = x2, it follows that y = 0 when x = 0 and y = 1 when x = 1
∴ Points of intersection between the two curves are (0,0) and (1,1)
Using intersection points, the region bounded by the two curves becomes;