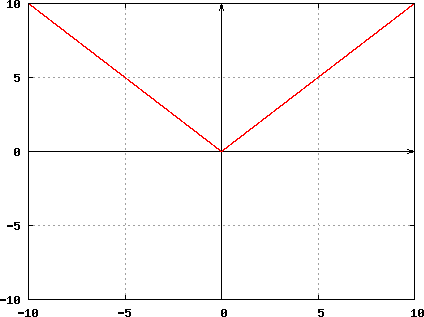
Continuity & Differentiability
If y = f (x) is differentiable at a, then f must also be continuous at a. However, if a function is continuous at a point, it may not be differentiable there.
Example #1:
Consider the step function f which returns a value, say 1, for
all x less than a, and returns a different value, say 5, for all
x greater than or equal to a. This function does not have a derivative at the marked point, as the function is
not continuous there.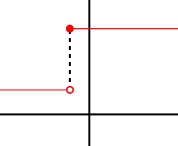
Example #2: