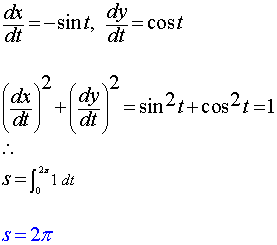Integrals: Length of a Curve
For function f(x) such
that f(x) and f′(x) are continuous on [a, b] . The length
s of the part of the graph of f between x = a and x = b is found by the formula
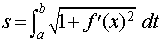
For smooth curve
defined parametrically by
Its length is equal to
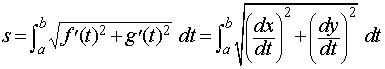
Example:
Solution:
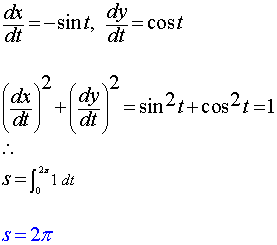
x = f(t), y = g(t)
a ≤ t ≤ b
Its length is equal to
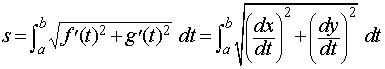
Example:
Determine the length of the curve defined by
x = cos t, y = sin t, 0 ≤ t ≤ 2π
x = cos t, y = sin t, 0 ≤ t ≤ 2π
Solution: