Skip to content
Subjects
Resources

    Double Integrals: Properties


    Various properties of double integrals are analogous to those for single integrals:
    • For f and g continuous in region D with c as rational number:   
    ∫∫D(f + g) dA = ∫∫D f dA + ∫∫D g dA
           
    ∫∫D cf dA = c ∫∫D f dA

    • For f continuous in region D, where D = D1 ∪ D2 where D1 and D2 are non-overlapping regions whose union is D:  
    ∫∫D f dA = ∫∫D1 f dA + ∫∫D2 f dA

    Example:

     For the region D bounded by y = 1 and y = x2, calculate ∫∫D (x + y) dx dy
    Solution:

    The region D may be illustrated as:



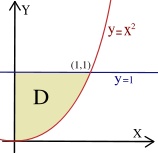
    Viewing the illustration, y = 1 and y = x2, the functions intersect at (1,1).  In addition, the limits of integration for x and y may be stated as:
    • x:  x = 0 to x = 1
    • y:  y = x2 to y =1
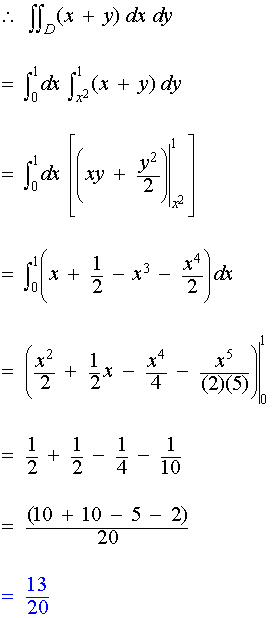
    with region more formally written as D = {(x,y):  y = x2; 0 ≤ x ≤ 1}

                                                                                                     
    Related Topics: