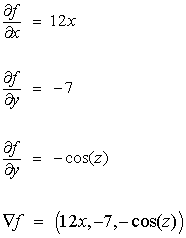Gradient of a Scalar Function
The gradient of a scalar function f(x) with respect to a vector variable x = (x1, x2, ..., xn) is denoted by ∇f where ∇ denotes the vector differential operator del. By definition, the gradient is a vector field whose components are the partial derivatives of f:
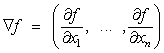
The form of the gradient depends on the coordinate system used.
For Cartesian Coordinates:
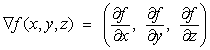
For Cylindrical Coordinates:
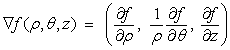
(where θ is the azimuthal angle and z is the axial coordinate)
For Spherical Coordinates:
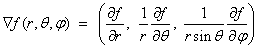
(where θ is the azimuthal angle and φ is the polar angle).
Example:
Find the gradient of the function f(x,y,z) = 6x2 - 7y - sin(z) in Cartesian coordinates
Solution:
Computing partial derivates: