Green's Theorem
Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C. It is the two-dimensional special case of the more general Stokes' theorem.
Let F(x) = (F(x,y), G(x,y)) be a vector field with continuous partial derivates in region D. If C is the boundar of D oriented clockwise, then:
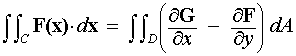
Example:
Evaluate the line integral of F(x,y) = (x - y, x + y) around the circle C: x = cos t, y = sin t for 0 ≤ t ≤ 2π
Solution:
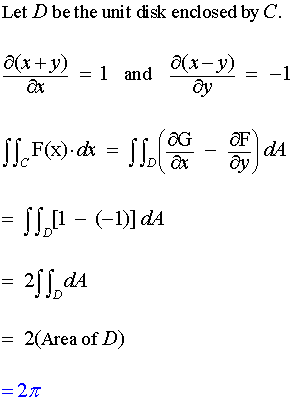
Related Topics:


