Hyperbolic Functions
Hyperbolic functions may be introduced by presenting their similarity to trigonometric functions.
Recalling from trigonometry that any point (x, y) on the unit circle, x2 + y2 =1, is represented by x = cos t and y = sin t, hyperbolic functions may be used to denote any point (x, y) on the unit hyperbola expressed by x2 − y2 =1. Specifically, the hyperbolic cosine and hyperbolic sine may be used to represent x and y respectively as x = cosh t and y = sinh t.
The hyperbolic functions (e.g., hyperbolic sine, hyperbolic cosine) are defined by:
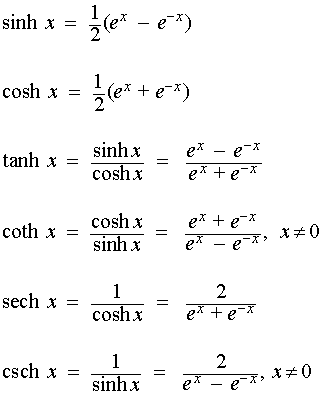
Similar to trigonometric functions, a fundamental identity exists for hyperbolic functions:
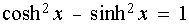
Derivatives of the hyperbolic functions are provided below:
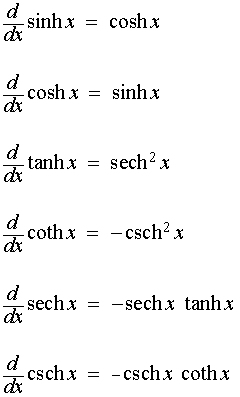
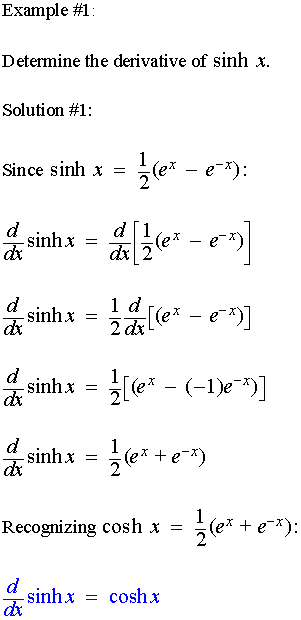
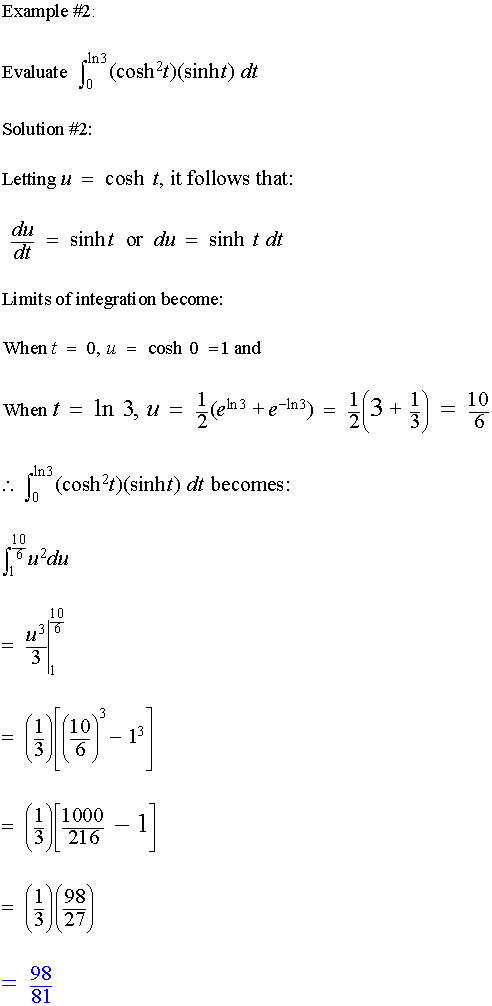
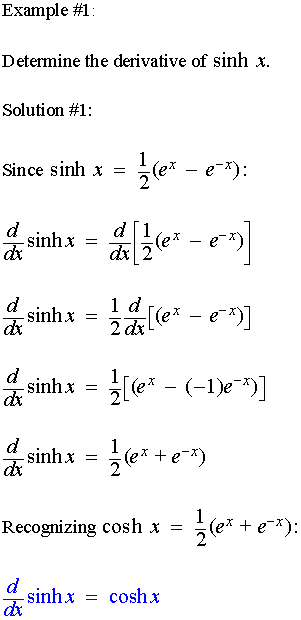
Related Topics:


