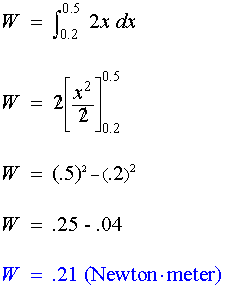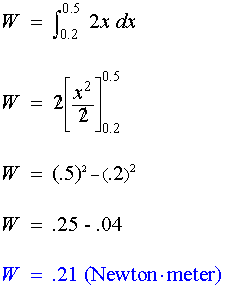Integrals: Work as an Integral
The work, W, performed moving an object from x=a to x=b by a force F(x) may be attained by the following: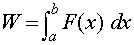
Example:
A spring exerts a restoring force of 0.2 newtons when it is compressed 0.4 meters. How much work is done compressing the spring an addition 0.3 meters?
Solution:
Using Hooke's Law, which states the force of compression (opposite direction to restoring force) is governed by:
As the spring constant has been determined, F(x) may be rewritten as:
Using Hooke's Law, which states the force of compression (opposite direction to restoring force) is governed by:
F(x) = kx for
spring constant, k,
where k > 0
As spring exerts a restoring force of 0.4 newtons for compression of 0.2 meters, it follows that F(0.2) = 0.4:
0.4 = k(0.2)
k = 2
k = 2
As the spring constant has been determined, F(x) may be rewritten as:
F(x) = 2x
The work done to compress the
spring an additional 0.3 meters (i.e., moving the spring from 0.2
meters to 0.5 meters) may be determined as follows: