Applications of Differentiation: Second Derivative Test
The Second Derivative Test may be used to determine extreme values of a function. Specifically, for critical point c of function f whose second derivative f '' is continuous and f ''(c) = 0:
- For f ''(c) > 0, f (c) is a local minimum,
- For f ''(c) < 0, f (c) is a local maximum,
- For f ''(c) = 0, test is inconclusive
Example:
Find the extreme values and
their locations regarding f
(x) =
2x3
−
3x2 using
the Second
Derivative Test.
Solution:
f (1) = 2(1)3 − 3(1)2 = 2 − 3 = −1
∴ Local maximum occurs at x = 0 with f (x) = 0 and local minimum occurs at x = 1 with f (x) = −1
This solution may be confirmed by examining the graph of f (x) = 2x3 − 3x2 depicted below:
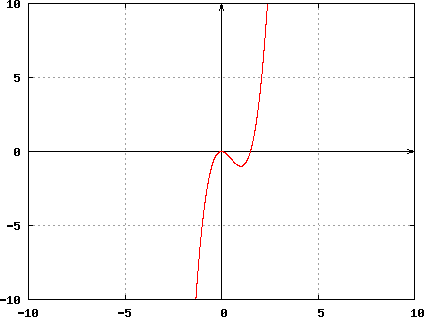
f '(x) = 6x2
−
6x
f ''(x) = 12x − 6
Can determine critical points by setting f '(x) = 0 and solving for x:
f '(x) = 6x2 − 6x = 0
6x(x − 1) = 0
∴ x = 0 and x =1 are critical points
Can use Second Derivative Test to test for extreme values:
f ''(0) = 12(0) − 6 = − 6 < 0 ⇒ x = 0 is local maximum
f ''(1) = 12(1) − 6 = 6 > 0 ⇒ x = 0 is local minimum
Value of local maximum at x = 0:
f (0) = 2(0)3 − 3(0)2 = 0
Value of local minimum at x = 1:
f ''(x) = 12x − 6
Can determine critical points by setting f '(x) = 0 and solving for x:
f '(x) = 6x2 − 6x = 0
6x(x − 1) = 0
∴ x = 0 and x =1 are critical points
Can use Second Derivative Test to test for extreme values:
f ''(0) = 12(0) − 6 = − 6 < 0 ⇒ x = 0 is local maximum
f ''(1) = 12(1) − 6 = 6 > 0 ⇒ x = 0 is local minimum
Value of local maximum at x = 0:
f (0) = 2(0)3 − 3(0)2 = 0
Value of local minimum at x = 1:
f (1) = 2(1)3 − 3(1)2 = 2 − 3 = −1
∴ Local maximum occurs at x = 0 with f (x) = 0 and local minimum occurs at x = 1 with f (x) = −1
This solution may be confirmed by examining the graph of f (x) = 2x3 − 3x2 depicted below:

Related Topic:


