Taylor's Formula
If n ≥ 0 is an integer and f is a function which is n times continuously differentiable on the closed interval [a, x] and n + 1 times differentiable on the open interval (a, x), then we have

In the above formula, n! denotes the factorial of
n, and Rn is a remainder term, denoting the difference
between the Taylor polynomial of degree n and the original function. The
remainder term Rn depends on x and is small if x
is close enough to a. Several expressions are available for it.
The Lagrange form of the remainder term states that there exists a number c between a and x such that
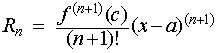
The integral form of the remainder term is
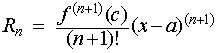
Related Topics:
The Lagrange form of the remainder term states that there exists a number c between a and x such that
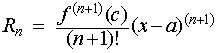
The Cauchy form of the remainder term states
that there exists a number c between a and x such that
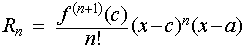
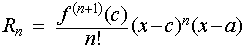
The integral form of the remainder term is
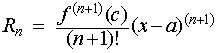
Related Topics:


