Skip to content
Subjects
Resources

    Integrals: Volume by Cylindrical Disks


    Let f (x) be continuous and nonnegative in [a,b].  When the region under the graph y = f(x), a ≤ x ≤ b is rotated about the x-axis, a solid of revolution is generated whose volume is


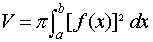
    Example:

    Find the volume of the solid generated by rotating the region under y = x2, 0 ≤ x ≤4 about the x-axis.

    Solution:


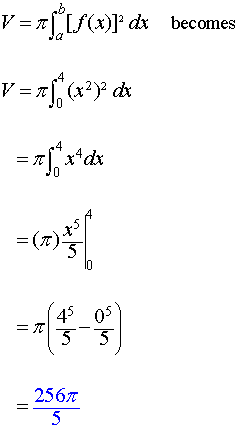
    Related Topic: