Linear Second-Order Equations with Constant Coefficients
Homogeneous linear differential equations of the form
L(y) = a(x)y'' + b(x)y' + c(x)y
= 0
where a(x), b(x), and c(x) are constants (i.e., a(x) = a, b(x) = b, and c(x) = c) may be rewritten as:
ay'' + by' + cy = 0
Letting y = erx, it follows that y' = rerx and y'' = r2erx . After substiting these variables into the above equation, results in the following:
ar2erx + brerx + cerx = 0
erx(ar2 + br + c) = 0
erx(ar2 + br + c) = 0
Therefore, erx is a solution if
and only if r is a root of the characteristic
equation:
ar2
+ br + c =
0
Two distinct conjugate complex roots r ± vi yielding the following solution:
y = erx (c1 cos(vx) + c2 sin(vx))
Example:
Solution:
The roots of the
characteristic equation are provided by the quadratic formula:
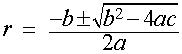
y = c1er1x + c2er2x
Two real and identical roots r1 and r2 = r yielding the following solution:
y = c1erx + c2xerx
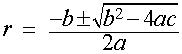
1) For the
discriminant b2 − 4ac > 0:
y = c1er1x + c2er2x
2) For the
discriminant b2 − 4ac = 0:
Two real and identical roots r1 and r2 = r yielding the following solution:
y = c1erx + c2xerx
3) For the
discriminant b2 − 4ac < 0:
Two distinct conjugate complex roots r ± vi yielding the following solution:
y = erx (c1 cos(vx) + c2 sin(vx))
Example:
Solve
y'' − 5y' − 6y
= 0
Solution:
As a = 1, b = −5, c = −6, resulting
characteristic equation is:
r2 − 5r − 6 = 0
Roots of above equation may be determined to be r1 = −1 and r2 = 6
Therefore, solutions of the differential equation are e-x and e6x with the general solution provied by:
y(x) = c1e-x + c2e6x
r2 − 5r − 6 = 0
Roots of above equation may be determined to be r1 = −1 and r2 = 6
Therefore, solutions of the differential equation are e-x and e6x with the general solution provied by:
y(x) = c1e-x + c2e6x


