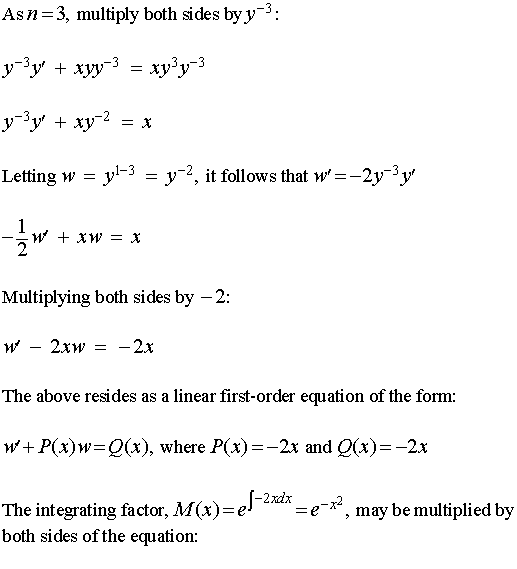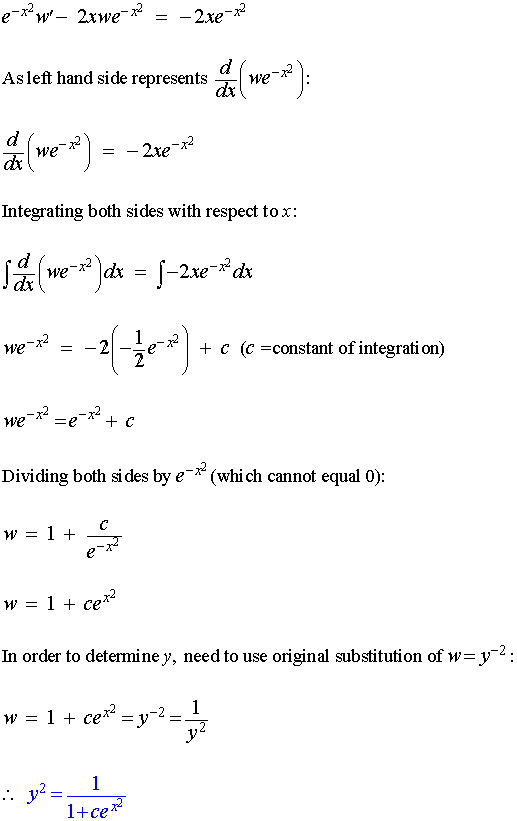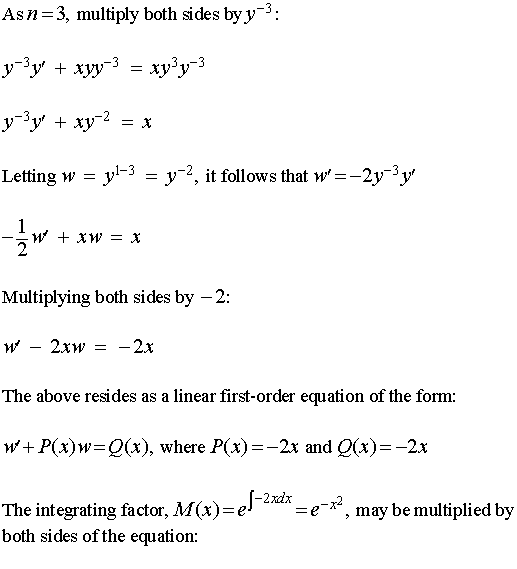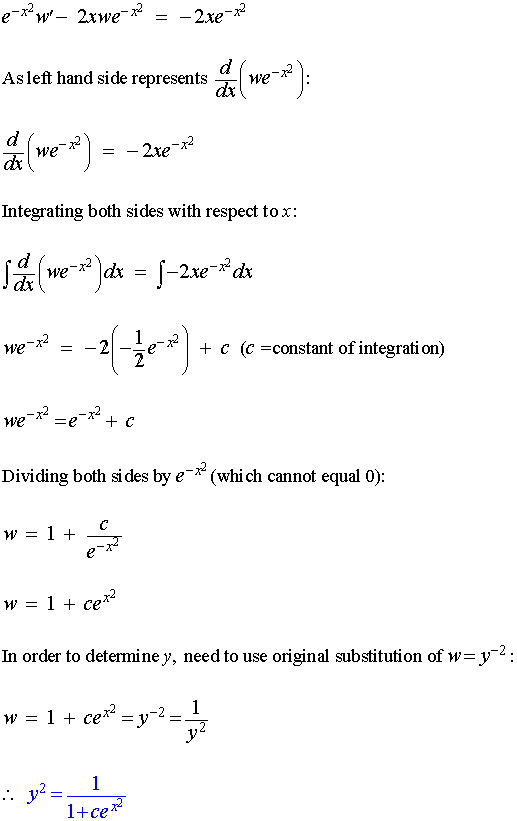Bernoulli Differential Equations
Bernoulli differential equations have the form:
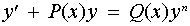
where n represents a real number. For n = 0, Bernoulli's equation reduces to a linear first-order differential equation.
Bernoulli differential equations may be solved by initially mulitplying both sides by y-n:
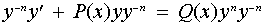
Substituting w = y1-n (with w' = (1 - n)y-n y' ), the above equation becomes:
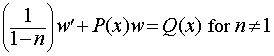
Bernoulli differential equations may be solved by initially mulitplying both sides by y-n:
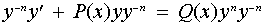
Substituting w = y1-n (with w' = (1 - n)y-n y' ), the above equation becomes:
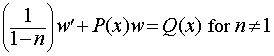
The above equation may be solved for w(x) using techniques for linear differential equations and solving for y.
Example:
Solve the equation y' + xy = xy3
Solution: