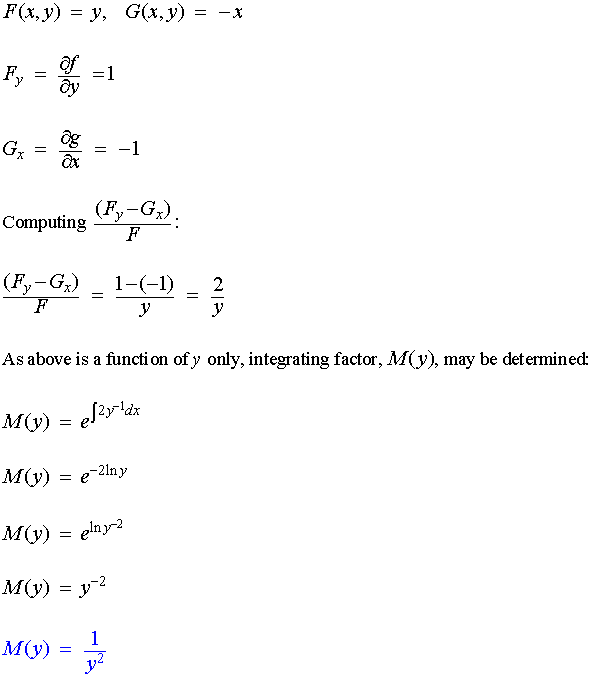Integrating Factors
If the differential equation
F(x,y) dx + G(x,y) dy = 0
is not exact, it is
possible to convert it to an exact different equation by multiplication
of an integrating factor.
By definition, if the above differential equation is not exact, it follows that Fy ≠ Gx, and consequently, Fy − Gx ≠ 0, in addition to Gx − Fy ≠ 0
If (Fy − Gx)/G defined as h(x) is a function of x only, integrating factor denoted by M(x):
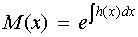
If (Fy − Gx)/F defined as k(y) is a function of y only, integrating factor denoted by M(y):
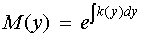
Example:
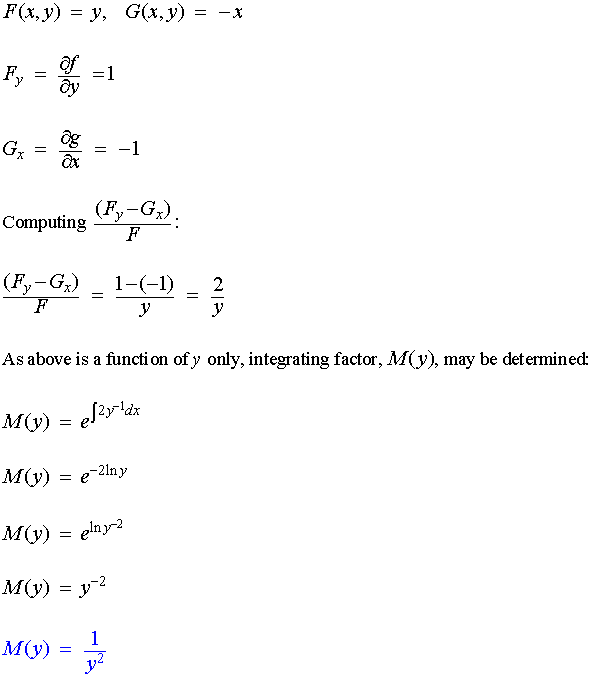
By definition, if the above differential equation is not exact, it follows that Fy ≠ Gx, and consequently, Fy − Gx ≠ 0, in addition to Gx − Fy ≠ 0
If (Fy − Gx)/G defined as h(x) is a function of x only, integrating factor denoted by M(x):
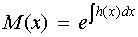
If (Fy − Gx)/F defined as k(y) is a function of y only, integrating factor denoted by M(y):
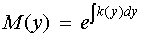
Example:
Find the integrating factor for the differential equation y dx - x dy = 0
Solution: