Equilateral Triangles
Equilateral triangles possess sides all of equal length. In addition, equilateral triangles are also an equiangular polygons (i.e. all internal angles are equal, specifically 60°)
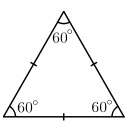
Example:
For the equilateral
triangle depicted below, determine the angle x and length from A
to B and length from B to C.
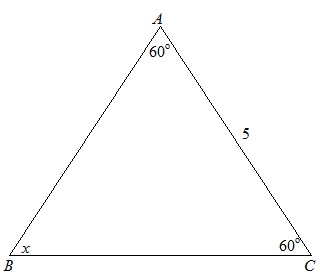
Solution:
As the triangle is
equilateral,
all sides are equal. Therefore,
AB = BC = AC
∴ AB = BC = 5
As the triangle is equilateral, all angles are equal. Therefore,
m∠x = 60°
Alternatively, the sum of interior angles for a triangle equals 180°:
m∠x + 60° + 60° = 180°
m∠x = 180° − 60° − 60°
m∠x = 60°
AB = BC = AC
∴ AB = BC = 5
As the triangle is equilateral, all angles are equal. Therefore,
m∠x = 60°
Alternatively, the sum of interior angles for a triangle equals 180°:
m∠x + 60° + 60° = 180°
m∠x = 180° − 60° − 60°
m∠x = 60°
Related Topics:


