Skip to content
Resources

    Hypergeometric Distribution


    The hypergeometric distribution is a discrete probability distribution that describes the number of successes in a sequence of n draws from a finite population without replacement.

    For a population of N objects containing m defective components, it follows the remaining N − m components are non-defective.  The hypergeometric distribution describes the probability that in a sample of n distinctive objects drawn from the shipment exactly k objects are defective.

    In general, a random variable X possessing a hypergeometric distribution with parameters N, m and n, the probability of getting exactly k successes is given by:



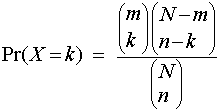
    The mean and variance of hypergeometric distribution are listed below:
    Example:

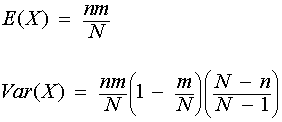
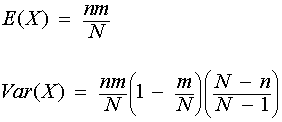
    Calculate the mean and variance of a hypergeometric random variable for parameters N = 700, m = 35, and n = 20.
    Solution:




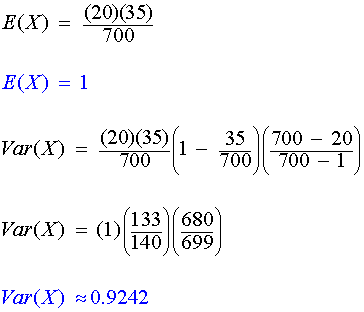
    Related Topics: