Joint Cumulative Distribution Function
A joint cumulative distribution function for two random variables X and Y is defined by:
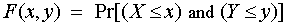
For two continuous random variables:
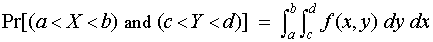
For two discrete random variables, it is beneficial to generate a table of probabilities and address the cumulative probability for each potential range of x and y.
Example:
Given the joint probability density function in tabular form, determine the joint cumulative distrubution function.
| Y = 2 | Y = 4 | Y = 6 | Y = 8 | |
| X = 1 | 0 | 0.1 | 0 | 0.1 |
| X = 3 | 0 | 0 | 0.2 | 0 |
| X = 5 | 0.3 | 0 | 0 | 0.15 |
| X = 7 | 0 | 0 | 0.15 |
0 |
Solution:
Using the given table of probabilities for each potential range of x and y, the joint cumulative distribution function may be constucted in tabular form:
| y < 2 | 2 ≤ y < 4 | 4 ≤ y < 6 | 6 ≤ y < 8 | y ≤ 8 | |
| x < 1 | 0 | 0 | 0 | 0 | 0 |
| 1 ≤ x < 3 | 0 | 0 | 0.1 | 0.1 | 0.2 |
| 3 ≤ x < 5 | 0 | 0 | 0.1 | 0.3 | 0.4 |
| 5 ≤ x < 7 | 0 | 0.3 | 0.4 | 0.6 | 0.85 |
| x ≤ 7 | 0 | 0.3 | 0.4 | 0.75 | 1 |


