Skip to content
Resources

    Correlation


    Correlation measures the strength regarding relationship between two random variables. The correlation coefficient of two random variables X and Y is represented by either

    r(X, Y) or ρ(X, Y)  

    The representation of r(X, Y) is utilized for correlation of sample data while ρ(X, Y) is employed for correlation of population data where ρ denotes the Greek letter rho.



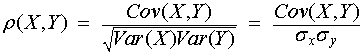
    The measure of correlation always resides between −1 and 1.  When Cov(X, Y) = 0, ρ(X, Y) = 0.

    Example:

    Determine the correlation between two random variables X and Y representing the numbers on the top and bottom of a fair die respectively.

    Solution:
    Using the fact that top and bottom numbers of dice always equal seven, in conjunction with the knowledge regarding a probability of 1/6 for each possible outcome for a fair die, it follows that:

    x y xy x2 y2 Pr(X=x) and Pr(Y=y)
    1 6 6 1 36 1/6
    2 5 10 4 25 1/6
    3 4 12 9 16 1/6
    4 3 12 16 9 1/6
    5 2 10 25 4 1/6
    6 1 6 35 1 1/6

    Using the entries above:

    E(X) = (1)(1/6) + (2)(1/6) + (3)(1/6) + (4)(1/6) + (5)(1/6) + (6)(1/6)

    E(X) = (1 + 2 + 3+ 4 + 5 + 6)/6

    E(X) = 21/6

    E(X) = 7/2 = 3.5


    E(Y) = (6)(1/6) + (5)(1/6) + (4)(1/6) + (3)(1/6) + (2)(1/6) + (1)(1/6)

    E(Y) = (6 + 5 + 4+ 3 + 2 + 1)/6

    E(Y) = 21/6

    E(Y) = 7/2 = 3.5


    E(XY) = (6)(1/6) + (10)(1/6) + (12)(1/6) + (12)(1/6) + (10)(1/6) + (6)(1/6)

    E(XY) = (6 + 10 + 12 + 12 + 10 + 6)/6

    E(XY) = 56/6

    E(XY) = 28/3 = 9.3333


    E(X2) = (1)(1/6) + (4)(1/6) + (9)(1/6) + (16)(1/6) + (25)(1/6) + (36)(1/6)

    E(X2) = (1 + 4 + 9 + 16 + 25 + 36)/6

    E(X2) =  91/6 = 15.1667


    E(Y2) = (36)(1/6) + (25)(1/6) + (16)(1/6) + (9)(1/6) + (4)(1/6) + (1)(1/6)

    E(Y2) = (36 + 25 + 16 + 9 + 4 + 1)/6

    E(Y2) =  91/6 = 15.1667


    Employing Cov(X, Y) = E(XY) − E(X) E(Y):

    Cov(X, Y) = 9.3333 − (3.5)(3.5)

    Cov(X, Y) = 9.3333 − 12.25

    Cov(X, Y) = −2.9167

    Using Var(X) = E(X2)     − [E(X)]2

    Var(X) = 15.1667 − (3.5)2

    Var(X) = 2.9167

    Taking sqaure root of Var(X), we obtain     σx = 1.7078

    Similarly, for random variable Y:

    Var(Y) = 15.1667 − (3.5)2

    Var(Y) = 2.9167

    Taking sqaure root of Var(Y), we obtain σy = 1.7078

    Using r(X, Y) = Cov(X, Y) /     σxσy:

    r(X, Y) = −2.9167/[(1.7078)(1.7078)]

    r(X, Y) = −1
    Related Topic: