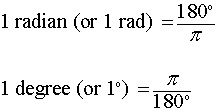Radians & Degrees
A radian is the angle subtended at the center of a circle by an arc of length equal to the radius of the circle.
More generally, the magnitude in radians of any angle subtended by two radii is equal to the ratio of the length of the enclosed arc to the radius of the circle; that is, θ = s /r, where θ is the subtended angle in radians, s is arc length, and r is radius. Conversely, the length of the enclosed arc is equal to the radius multiplied by the magnitude of the angle in radians, namely s = rθ.
It follows that the magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference divided by the radius, or 2πr /r, or 2π. Thus 2π radians is equal to 360 degrees, meaning that one radian is equal to 180/π degrees.